1.
Introducción
La
teoría general de sistemas enfocada en el desarrollo del pensamiento sistémico,
insiste en adoptar nuevos modelos teóricos, metodológicos y epistemológicos que
permitan la elaboración de propuestas didácticas acordes con la realidad de la
enseñanza y el aprendizaje, y posibiliten el diseño y la puesta en práctica de
modelos que permitan una intervención educativa más eficaz; lo que implicaría
una línea consciente y sistémica de componentes cognitivos, metacognitivos y
socioafectivos para la mejora de las habilidades de aprendizaje y del nivel de
procesamiento y manejo de la información, a fin de facilitar el logro de las
tareas por parte de los estudiantes (Corcino-Barrueta et al., 2021).
La necesidad
de incorporar al pensamiento sistémico en el desarrollo de problemas en la
complejidad, no puede más que imponerse de manera progresiva en un camino en
que surgen límites, insuficiencias y carencias del pensamiento simplificante,
propios de las estrategias de resolución de problemas matemáticos en el enfoque
del constructivismo; es decir, las condiciones en las cuales no es posible
dejar de considerar el desafío de lo complejo. En este escenario, se ejercita
un pensamiento dialogante y negociador con lo real, que integra los modos
simplificadores de pensar; rechazando las consecuencias mutilantes,
reduccionistas y unidimensionales de las situaciones problemas (Barragán Moyano
et al., 2018).
El presente
estudio identificó como problema, una inadecuada aplicación del modelo de
resolución de problemas matemáticos a causa de la exclusión del pensamiento
sistémico de la enseñanza y aprendizaje, en el que sus elementos tienen muy
poca relación con el constructivismo; contribuyendo al bajo logro de
aprendizajes en los estudiantes del tercer grado de secundaria de la I. E.
“Santa Rosa” - Tarapoto. Al respecto, Corcino-Barrueta et al. (2021) indican
que la educación debe modificar sus contenidos y aportes curriculares,
asumiendo una metodología didáctica dentro de un modelo sistémico, con una
visión integradora que relacione las partes en una totalidad y valore su
evolución en su entorno.
En el
desarrollo de la investigación, el escaso hábito de resolver problemas y el
desconocimiento de los contenidos matemáticos básicos para operativizar
estrategias algorítmicas de solución; fueron las limitaciones evidenciadas en
los estudiantes, que dificultaron la observación y recolección de los datos. Al
respecto, Donoso Osorio et al. (2020) explican que la resolución de un problema
es un proceso con una serie de pasos en complejidad progresiva durante su
desarrollo, en el que el estudiante integra la información textual con
conocimientos matemáticos necesarios al contexto problemático que permite la
solución; de lo contrario se hace dificultoso al resolver el problema.
Los objetivos
de la investigación fueron: analizar y medir la relación entre el pensamiento
sistémico y el modelo de resolución de problemas, determinar las causas de los
bajos logros en la resolución de problemas con el modelo constructivista;
diseñar un modelo basado en el pensamiento sistémico para la resolución de
problemas complejos de matemática.
Los resultados
de la investigación confirmaron la existencia de una relación muy alta y
positiva entre el pensamiento sistémico y la resolución de problemas. Su
importancia derivó en el planteamiento de un modelo de enseñanza-aprendizaje
basado en la concreción de los niveles de dominio del pensamiento sistémico y
la resolución de problema complejos de matemática, empleándose para el cual
Vensim PLE 7.3.5, como software de simulación dinámica.
2.
Materiales
y métodos
La investigación
desarrollada fue de tipo básica, nivel correlacional, con diseño no
experimental y descriptiva. La población en su totalidad fue tomada como
muestra censal y constituida por 163 estudiantes.
Se tomó como
referencia el marco teórico de Villa Sánchez & Poblete Ruiz (2017) para
elaborar las rúbricas de evaluación del pensamiento sistémico y de la
resolución de problemas que permitieron la medición de sus niveles de dominio,
respectivos; las cuales fueron sometidas al criterio de expertos; antes de su
aplicación. La recolección de los datos se realizó al observar el desempeño en
la resolución de problemas de matemática de cada estudiante de tercer grado de
secundaria, con edades desde los 14 hasta los 17 años de la I. E. “Santa Rosa”
- Tarapoto, en el año 2019.
Para lograr el
análisis y la medición de la relación entre el pensamiento sistémico y el
modelo de resolución de problemas, se han seguido los siguientes pasos:
aplicación de las dos rúbricas de evaluación, procesamiento de los datos
recolectados empleando Excel 2019 y SPSS 23, cálculo de coeficientes de
correlación “t” (tau b de Kendall) entre las variables estudiadas y sus niveles
correspondientes; y análisis, presentación y explicación de resultados basados
en los valores de coeficientes de correlación “t” obtenidos. Sáenz López &
Tamez González (2018) refieren que el coeficiente de correlación tau b de
Kendall es una medida no paramétrica de asociación para variables ordinales y
muestras pequeñas.
Para
determinar las causas académicas, materiales y metodológicas de los bajos
logros de aprendizaje en la resolución de problemas con el modelo
constructivista, se realizaron los pasos: observación de la situación actual,
aplicación del diagrama de Ishikawa para obtener el diagnóstico; y
sistematización de las causas. Gutiérrez Verde et al. (2020) explican que el
diagrama de Ishikawa o causa-efecto, representa gráficamente la relación que
existe entre algún efecto y el conjunto de factores causantes que intervienen o
influencian en una determinada característica.
Para diseñar
el modelo basado en el pensamiento sistémico en favor de la resolución de
problemas complejos de matemática se desarrollaron los pasos: revisión y
análisis de las propuestas de Villa Sánchez & Poblete Ruiz (2017), y de la
propuesta constructiva del Ministerio de Educación (2016), utilización del
diagnóstico de causas de bajos logros en resolución de problemas, y elaboración
del modelo con dinámica de sistemas fundamentado en Gil Vera & Gil Vera (2017)
como técnica de modelado de los problemas complejos de matemática; y desarrollo
de los modelos empleando el software Vensim PLE 7.3.5.
3.
Resultados
Tabla 1. Resultados de la correlación entre
las variables.
|
Variables
|
Correlación
|
|
Pensamiento
sistémico y resolución de problemas.
|
Muy
alta y positiva
|
|
Primer
y segundo nivel de dominio del pensamiento sistémico.
|
Muy
alta y positiva
|
|
Segundo
y tercer nivel de dominio del pensamiento sistémico.
|
Muy
alta y positiva
|
|
Primer
y segundo nivel de dominio de la resolución de problemas.
|
Alta
y positiva
|
|
Segundo
y tercer nivel de dominio de la resolución de problemas.
|
Alta
y positiva
|
|
Primer
nivel de dominio del pensamiento sistémico y la resolución de problemas.
|
Moderada
y positiva
|
|
Segundo
nivel de dominio del pensamiento sistémico y la resolución de problemas.
|
Muy
alta y positiva
|
|
Tercer
nivel de dominio del pensamiento sistémico y la resolución de problemas.
|
Alta
y positiva
|
Los resultados de la correlación entre las variables son: muy
alta y positiva entre el pensamiento sistémico y la resolución de problemas,
muy alta y positiva entre el primer y segundo nivel de dominio del pensamiento
sistémico, muy alta y positiva entre el segundo y tercer nivel de dominio del
pensamiento sistémico, alta y positiva entre el primer y segundo nivel de
dominio de la resolución de problemas.
Además de
correlaciones alta y positiva entre el segundo y tercer nivel de dominio de la
resolución de problemas, moderada y positiva entre el primer nivel de dominio
del pensamiento sistémico y la resolución de problemas, muy alta y positiva
entre el segundo nivel de dominio del pensamiento sistémico y la resolución de
problemas, alta y positiva entre el tercer nivel de dominio del pensamiento
sistémico y la resolución de problemas.
Tabla 2. Resultados de la medición de la correlación
entre las variables.
|
Variables
|
Valor “t”
|
|
Pensamiento
sistémico y resolución de problemas.
|
0,918
|
|
Primer
y segundo nivel de dominio del pensamiento sistémico.
|
1
|
|
Segundo
y tercer nivel de dominio del pensamiento sistémico.
|
1
|
|
Primer
y segundo nivel de dominio de la resolución de problemas.
|
0,831
|
|
Segundo
y tercer nivel de dominio de la resolución de problemas.
|
0,938
|
|
Primer
nivel de dominio del pensamiento sistémico y la resolución de problemas.
|
0,646
|
|
Segundo
nivel de dominio del pensamiento sistémico y la resolución de problemas.
|
0,934
|
|
Tercer
nivel de dominio del pensamiento sistémico y la resolución de problemas.
|
0,876
|
Los resultados de los valores de los
coeficientes “t” (tau b de Kendall) de la medición de la correlación entre las
variables son: 0,918 entre el pensamiento sistémico y la resolución de
problemas, 1 entre el primer y segundo nivel de dominio del pensamiento
sistémico, 1 entre el segundo y tercer nivel de dominio del pensamiento
sistémico; 0,831 entre el primer y segundo nivel de dominio de la resolución de
problemas.
Asimismo;
0,938 entre el segundo y tercer nivel de dominio de la resolución de problemas;
0,646 entre el primer nivel de dominio del pensamiento sistémico y la
resolución de problemas; 0,934 entre el segundo nivel de dominio del
pensamiento sistémico y la resolución de problemas; y 0,876 entre el tercer
nivel de dominio del pensamiento sistémico y la resolución de problemas.
Tabla 3. Causas de bajos logros en la
resolución de problemas con el modelo constructivista.
|
Académicas
|
Desinterés
de los estudiantes por participar en el desarrollo de la clase.
|
|
Prevalencia
en los estudiantes del individualismo que el trabajo cooperativo.
|
|
Desistimiento
por concebir un horizonte en común en el trabajo colaborativo.
|
|
Resistencia
de los estudiantes para socializar los productos y resultados.
|
|
Poco
conocimiento y manejo de los contenidos matemáticos.
|
|
Materiales
|
Aulas
inadecuadas para las clases.
|
|
Textos
escolares con predominio del conocimiento científico memorístico.
|
|
Situaciones
problemáticas orientadas y cerradas a la práctica constructivista.
|
|
Cuaderno
de trabajo con problemas ajenos a nuestro contexto.
|
|
Metodológicas
|
Evaluación
centrada en la medición de conocimientos.
|
|
Omisión
de la retroalimentación reflexiva.
|
|
Priorización
y prevalencia del conductismo en la resolución de problemas.
|
|
Priorización
por el desarrollo de algoritmos.
|
|
Ejecución
didáctica centrada en el docente como expositor de conocimientos.
|
|
Desarrollo
del enfoque de resolución de problemas solo con el constructivismo.
|
|
Desconocimiento
de la información necesaria relacionada con el modelo constructivista.
|
|
Resistencia
docente por el desarrollo de estrategias de enseñanza-aprendizaje centrado en
la resolución de problemas.
|
En lo académico, las causas de los
bajos logros en la resolución de problemas por parte de los estudiantes son:
desinterés por participar en el desarrollo de la clase, prevalencia del
individualismo que el trabajo colaborativo, desistimiento por concebir un
horizonte en común en el trabajo colaborativo, resistencia para socializar los
productos y resultados y poco conocimiento y manejo de los contenidos
matemáticos.
En cuanto a
las condiciones materiales las causas son: aulas inadecuadas para las clases,
textos escolares con predominio del conocimiento científico y memorístico,
situaciones problemáticas orientadas y cerradas a la práctica constructivista y
cuadernos de trabajo con problemas ajenos a nuestro contexto.
Sobre los
aspectos metodológicos las causas son: evaluación centrada en la medición de
los conocimientos, omisión de la retroalimentación reflexiva, priorización y
prevalencia del conductismo en la resolución de los problemas, priorización por
el desarrollo de algoritmos, ejecución didáctica centrada en el docente como
expositor de conocimientos, desarrollo del enfoque de la resolución de
problemas solo centrado en el constructivismo, desconocimiento de la
información relacionada con el modelo constructivista, resistencia docente por
el desarrollo de estrategias de enseñanza-aprendizaje centrado en la resolución
de problemas.
Se diseñó un
modelo basado en el pensamiento sistémico para la resolución de problemas
complejos de matemática. Sus componentes permiten desarrollar sesiones de
aprendizaje en el que los estudiantes resuelven problemas complejos de
matemática en el marco del diseño curricular nacional y los estándares de
aprendizaje de la educación básica regular.
Figura 1. Modelo basado en el pensamiento sistémico para la resolución
de problemas complejos de matemática.
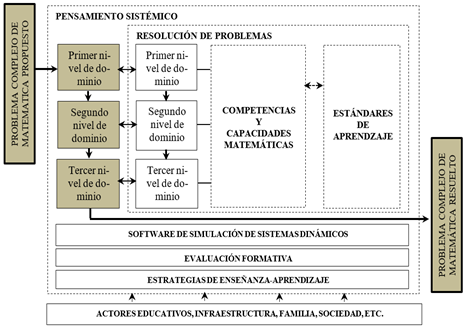
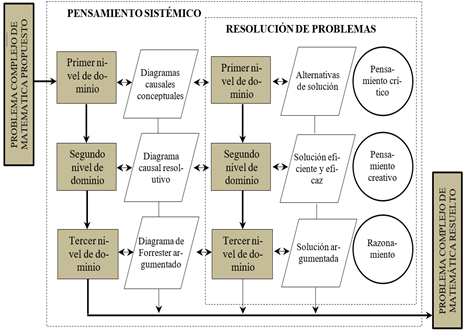
Figura 2. Metodología de aplicación práctica del modelo basado en el
pensamiento sistémico para la resolución de problemas complejos de matemática
en estudiantes del 3er grado de la I. E. “Santa Rosa”.
El pensamiento
sistémico es el macrosistema del modelo con los componentes resolución de
problemas, competencias y capacidades matemáticas, estándares de aprendizaje y
estrategias de enseñanza-aprendizaje. Comprende la concreción de tres niveles
de dominio, el primero inicia el proceso de resolución del problema complejo
propuesto, el segundo permite decidir y consolidar la construcción de una
solución eficiente y eficaz, y el tercero concreta la solución del problema
complejo, resuelto con procedimientos formales simulados a través de un
software de simulación dinámica.
La resolución
de problemas constituye el mesosistema del modelo, que además de las
competencias y capacidades matemáticas y los estándares de aprendizaje,
concreta el desarrollo de sus tres niveles de dominio. En el primero se
identifica y analiza el problema complejo planteado y propone alternativas de
solución, en el segundo se analizan nuevas alternativas de solución y se
construye una solución eficiente y eficaz, y en el tercero se propone una o más
soluciones referidos a otros contextos o ámbitos de la realidad, relacionados
con el problema complejo propuesto. Los niveles de dominio de la resolución de
problemas se desarrollan simultáneamente a los del pensamiento sistémico.
El software de
simulación de sistemas dinámicos es el componente tecnológico transversal que
se utiliza desde el inicio de la resolución del problema e interviene en los
tres niveles de dominio del pensamiento sistémico y de lo resolución de
problemas, favorece en la intervención didáctica para lograr las competencias y
capacidades del área de matemática, con la provisión de las herramientas del pensamiento
sistémico que se emplean al resolver un problema complejo de matemática.
La evaluación
formativa es un componente transversal que interactúa durante el proceso de
resolución del problema complejo, interviniendo en todos los componentes del
modelo. Permite la retroalimentación reflexiva durante el desarrollo de los
niveles de dominio del pensamiento sistémico y de la resolución de problemas, a
fin de corregir oportuna y recurrentemente los errores o inconvenientes en la
aplicación del conocimiento matemático y los procedimientos didácticos
soportados en diagramas causales y de Forrester.
Las
estrategias de enseñanza-aprendizaje es un componente transversal a todo el
proceso de la resolución del problema complejo, concebido en los enfoques del
pensamiento sistémico y constructivismo. Para la planificación y ejecución se
considera estrategias didácticas en contextos colaborativos, en el que se
emplean a los diagramas causales como las herramientas del pensamiento
sistémico, las estrategias de enseñanza-aprendizaje y los problemas
contextuales reales e inmediatos a los estudiantes.
Como el modelo
está basado en el pensamiento sistémico para la resolución de problemas
dinámicos o complejos de matemática, está concebido como un sistema abierto en
el que otros factores lo afectan. La influencia de otros sistemas o subsistemas
externos, inciden en la intervención pedagógica que el docente realiza en el
proceso de enseñanza de la resolución del problema complejo. Estos agentes externos
son: los actores educativos, la infraestructura actual, las otras áreas del
conocimiento, los recursos y materiales disponibles, y el contexto familiar y
social de los estudiantes.
En cuanto al
fundamento, la intervención didáctica planteada por Montenegro & Schroeder (2020)
en su investigación coincide con el modelo propuesto, dado que, el pensamiento
sistémico es concebido como condición relevante para el aprendizaje y
profundiza sus dimensiones: configuración del problema, abarcabilidad de
factores, supuestos de causalidad y soportes simbólicos apelados; que
tácitamente, también soportan la propuesta de enseñanza y aprendizaje de la
resolución de problemas complejos de matemática de este estudio. El pensamiento
sistémico se presenta como un patrón autoorganizado y se manifiesta como
emergente interaccional y contextual más que como una competencia individual.
4.
Discusión
La alta y muy alta
correlación entre las variables y subvariables del pensamiento sistémico
(tablas 1 y 2) confirman la asociación directa entre ellas. A mayor dominio del
pensamiento sistémico y de sus niveles, es también mayor el dominio de la
resolución de problemas y de sus niveles; lo que garantiza un manejo adecuado
de las herramientas del pensamiento sistémico. Lo encontrado coincide con
Barragán et al. (2018) en lo referido a que, si el proceso de enseñanza es
organizado correctamente y en forma sistemática en niveles progresivos de
logro, garantiza el desarrollo del pensamiento complejo desde la
sistematización de la enseñanza de la matemática.
Los bajos
logros en la resolución de problemas de matemática en los estudiantes del
tercer grado de educación secundaria de la I. E. “Santa Rosa”, se deben a
causas académicas, materiales y metodológicas (tabla 3). Corcino-Barrueta et
al. (2021), enfatiza lo metodológico y manifiesta la necesidad de desarrollar
procesos educativos de forma sistémica y holística, en el que la acción docente
se integra al conjunto de todos los actores y recursos tangibles o no al acto
de enseñar, y que son factores determinantes en el aprendizaje de conocimientos
conceptuales, procedimentales y actitudinales utilizados en la resolución de
problemas matemáticos, en combinación con herramientas del pensamiento
sistémico.
El empleo
inadecuado de un modelo de resolución de problemas centrado en el
constructivismo sin el enfoque del pensamiento sistémico y sus herramientas,
han conllevado a que lo estudiantes evidencien dificultades en la resolución de
problemas. Al respecto, se ha propuesto un modelo (figuras 1, 2) en el que el pensamiento
sistémico se incorpora en las estrategias de enseñanza-aprendizaje para
resolver de problemas complejos de matemática; Donoso Osorio et al. (2020)
coinciden en considerar un enfoque holístico e integrador en los procesos
crecientes en complejidad al resolver un problema, y propenden a potenciar la
influencia de la intervención pedagógica sobre los logros de aprendizaje que se
esperan.
El modelo
propuesto recoge el aporte de los diagramas causales y el análisis en la
complejidad para emplearla en las estrategias de enseñanza-aprendizaje al
resolver el problema matemático, el cual favorece al desarrollo de la
creatividad, como parte del pensamiento complejo; y al tomar en cuenta las
herramientas que emplea el pensamiento sistémico, en el proceso de enseñanza y
aprendizaje para la resolución de un problema matemático.
5.
Conclusión
Existe una correlación (t
= 0,918) muy alta y positiva entre el pensamiento sistémico y la resolución de
problemas matemáticos. Existen correlaciones muy altas y positivas del primer
al segundo nivel de dominio (t = 1), y del segundo al tercer nivel de dominio
(t = 1) del pensamiento sistémico. Existen correlaciones altas y positivas del
primer al segundo nivel de dominio (t = 0,831), y del segundo al tercer nivel
de dominio (t = 0,938) de la resolución de problemas.
La correlación
entre el primer nivel de dominio del pensamiento sistémico y de la resolución
de problemas es moderada y positiva (t = 0,646). La correlación entre el
segundo nivel de dominio del pensamiento sistémico y de la resolución de
problemas es muy alta y positiva (t = 0,934). La correlación entre el tercer
nivel de dominio del pensamiento sistémico y de la resolución de problemas es
alta y positiva (t = 0,876).
Las causas
académicas que ocasionan bajos logros en la resolución de problemas matemáticos
con el modelo constructivista son: el desinterés por participar en el
desarrollo de las clases y la prevalencia del individualismo, el desistimiento
por concebir un horizonte común de solución, la resistencia a la socialización
de resultados; y el poco conocimiento y manejo de los contenidos matemáticos.
Las causas
materiales que ocasionan bajos logros en la resolución de problemas matemáticos
con el modelo constructivista son: el uso de textos escolares predominantemente
memorísticos, el planteo de problemas orientados y cerrados solo a la práctica
constructivista, y el empleo de cuadernos de trabajo con problemas ajenos al
contexto.
Las causas
metodológicas que ocasionan bajos logros en la resolución de problemas matemáticos
con el modelo constructivista son: las evaluaciones que miden solo conocimientos
y no considera a la retroalimentación reflexiva, la priorización y prevalencia
del conductismo, la priorización de la práctica algorítmica, la ejecución
didáctica centrada en el docente, el enfoque de resolución de problemas
limitado al modelo constructivista, el desconocimiento de la información sobre
el modelo constructivista, y la resistencia del docente por el desarrollo de
estrategias de enseñanza-aprendizaje en el enfoque problémico.
El modelo
basado en el enfoque del pensamiento sistémico en el que se emplean los
diagramas causales conceptuales, diagramas causales resolutivos y diagramas de
Fórrester argumentados; permiten la integración, articulación e interrelación
con los componentes o elementos de la resolución de problemas de matemática y
facilitan la solución de situaciones en contextos reales en la complejidad.
Referencias
bibliográficas
Barragán Moyano, V. E., Jaque Sandoval, J. E., & Acosta Patiño,
E. I. (2018). El pensamiento complejo desde la enseñanza de la Lógica
Matemática (Revisión). Revista Científico Educacional De La Provincia
Granma, 14(4), 169–181. https://revistas.udg.co.cu/index.php/roca/article/view/547
Corcino-Barrueta, F. E., Chamoli-Falcon, A. W.,
Otalora-Martinez, C. R., & Melgarejo-Figueroa, M. D. P. (2021). El modelo
sistémico de aprendizaje y enseñanza, como apoyo en la inserción laboral. Investigación
Valdizana, 15(1), 31–40. https://doi.org/10.33554/riv.15.1.798
Donoso Osorio, E., Valdés Morales, R. A., Cisternas Núñez,
P., & Cáceres Serrano, P. (2020). Enseñanza de la resolución de problemas
matemáticos: un análisis de correspondencias múltiples. Diálogos Sobre
Educación, 11(21), 1–22. https://doi.org/10.32870/dse.v0i21.629
Gil Vera, V. D., & Gil Vera, J. C. (2017). Seguridad
informática organizacional: un modelo de simulación basado en dinámica de
sistemas. Scientia et Technica, 22(2), 193–197. https://doi.org/10.22517/23447214.11371
Gutiérrez Verde, E., Rodríguez Ramos, P. A., & Lavado
Ruiz, C. (2018). Mejoras para elevar la disponibilidad de las unidades
acuáticas livianas. Ingenería Mecánica, 23(1), 1–8. https://ingenieriamecanica.cujae.edu.cu/index.php/revistaim/article/view/621
Ministerio de Educación. (2016). Educación Básica Regular.
Programa Curricular de Educación Secundaria. Talleres gráficas del Minedu. http://www.minedu.gob.pe/curriculo/pdf/03062016-programa-nivel-secundaria-ebr.pdf
Montenegro, G., & Schroeder, I. (2020). Dimensiones del
pensamiento sistémico aplicado: un estudio de casos múltiple desde la
perspectiva de sistemas complejos y el aprendizaje organizacional. Psicología,
Conocimiento y Sociedad, 10(2), 74–100. https://doi.org/10.26864/PCS.v10.n2.4
Sáenz López, K., & Tamez González, G. (2015). Métodos
y técnicas cualitativas y cuantitativas aplicables a la investigación en
ciencias sociales (1st ed.). Tirant lo Blanch.
Villa Sánchez, A., & Poblete Ruiz, M. (2013). Aprendizaje
basado en competencias. Una propuesta para la evaluación de las competencias
genéricas (3rd ed.). In E. Mensajero.
Financiamiento
Ninguno.
Conflicto de
intereses
El artículo no presenta
conflicto de intereses.
Contribución de autores
Montilla-García, Henrry: Investigador
y redactor del artículo.
![]() 0000-0001-8332-2643]1
0000-0001-8332-2643]1
